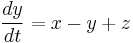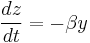Chua's circuit

Chua's circuit is a simple electronic circuit that exhibits classic chaos theory behavior. It was introduced in 1983 by Leon O. Chua, who was a visitor at Waseda University in Japan at that time.[1] The ease of construction of the circuit has made it a ubiquitous real-world example of a chaotic system, leading some to declare it "a paradigm for chaos."[2]

Contents

Chaotic criteria

An autonomous circuit made from standard components (resistors, capacitors, inductors) must satisfy three criteria before it can display chaotic behaviour. It must contain:

  1. one or more nonlinear elements
  2. one or more locally active resistors
  3. three or more energy-storage elements.

Chua's circuit is the simplest electronic circuit meeting these criteria. As shown in the figure, the energy storage elements are two capacitors (labeled C1 and C2) and an inductor (labeled L1). There is an active resistor (labeled R). There is a nonlinear resistor made of two linear resistors and two diodes. At the far right is a negative impedance converter made from three linear resistors and an operational amplifier.

Model

By means of the application of the laws of electromagnetism, the dynamics of Chua's circuit can be accurately modeled by means of a system of three nonlinear ordinary differential equations in the variables x(t), y(t) and z(t), which give the voltages across the capacitors C1 and C2, and the intensity of the electrical current in the inductor L1, respectively. These equations read:

\frac{dx}{dt}=\alpha [y-x-f(x)]
\frac{dy}{dt}=x-y%2Bz
\frac{dz}{dt}=-\beta y

The function f(x) describes the electrical response of the nonlinear resistor, and its shape depends on the particular configuration of its components. The parameters α and β are determined by the particular values of the circuit components.

A chaotic attractor, known as "The Double Scroll" because of its shape in the (x,y,z) space, was first observed in a circuit containing a nonlinear element such that f(x) was a 3-segment piecewise-linear function.[3]

The easy experimental implementation of the circuit, combined with the existence of a simple and accurate theoretical model, makes Chua's circuit a useful system to study many fundamental and applied issues of chaos theory. Because of this, it has been object of much study, and appears widely referenced in the literature. Moreover the Chua' s circuit can be easily realized by using a multilayer CNN (Cellular Nonlinear Networks). The CNN have been just invented by Leon Chua in 1988. To date, а huge number of various types of chaotic attractors in Chua's system has been discovered, which can be obtained numerically, with relative ease, by standard computational procedure (after transient process a trajectory, started from a point of unstable manifold in a small neighborhood of unstable zero equilibrium, reaches an attractor and computes it)[4]. Also, recently, a hidden Chua's attractor was discovered[5].

See also

References

  1. ^ Matsumoto, Takashi (December 1984). "A Chaotic Attractor from Chua's Circuit". IEEE Transactions on Circuits and Systems (IEEE) CAS-31 (12): 1055–1058. http://www.eecs.berkeley.edu/~chua/papers/Matsumoto84.pdf. Retrieved 2008-05-01. 
  2. ^ Madan, Rabinder N. (1993). Chua's circuit: a paradigm for chaos. River Edge, N.J.: World Scientific Publishing Company. ISBN 9810213662. 
  3. ^ Chua, Leon O.; Matsumoto, T., and Komuro, M. (August 1985). "The Double Scroll". IEEE Transactions on Circuits and Systems (IEEE) CAS-32 (8): 798–818. http://ieeexplore.ieee.org/iel5/31/23571/01085791.pdf. Retrieved 2008-05-01. 
  4. ^ Bilotta, E., Pantano, P. (2008). Gallery of Chua Attractors. World Scientific. ISBN 978-981-279-062-0. 
  5. ^ Leonov G.A., Vagaitsev V.I., Kuznetsov N.V. (2011). "Localization of hidden Chua's attractors". Physics Letters, Section A 375 (23): 2230–2233. doi:10.1016/j.physleta.2011.04.037. 

Books

External links